How to resolve deadlock in asynchronization code with async/await
分类于 专业技术
Background
In .NET, there are currently three main asynchronous programming models: Asynchronous Programming Model (APM), Event-based Asynchronous Pattern (EAP) and Task-based Asynchronous Pattern (TAP). The TAP is the latest technology that is based on the Task and Task<T> types (available since .NET 4.0) in the System.Threading.Tasks namespace. Programmers can also use async/await keywords to improve the code readability since C# 5.0. There is a MSDN article explaining on the interop of the TAP model with previous asynchronous models. When programming in an asynchronous way, programmers need to be very careful of the deadlock. In this post, a common deadlock issue in TAP is explained and solutions are provided to avoid it in both production code and unit tests.
Problem
Here is the code-behind of a form. There is a button named button1 and a text box named textbox1 on the form. When the button is clicked, it runs a long time job that is sleeping for 2 seconds and shows a message in the text box then.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
public partial class Form1 : Form { public Form1() { InitializeComponent(); } private void button1_Click(object sender, EventArgs e) { InvokeTask(); } public void InvokeTask() { textBox1.Text = $"Start task at {DateTime.Now.ToString("T")} and wait"; var task = DoLongTimeJob(); task.Wait(); textBox1.Text = $"Task finished at {DateTime.Now.ToString("T")}"; } public static async Task DoLongTimeJob() { await Task.Delay(TimeSpan.FromSeconds(2)); } } |
Investigation
As we all know, Windows applications is based on a single-threaded model. A message pump runs on the main thread which listens and dispatches messages to the different listeners. The above code run into a deadlock because of this. How does it happen?
On line 18, the main UI thread waits for the task to complete here. On line 25, the code were put on a different thread to run which just sleep for 2 seconds. After that, it tries to return back to the main UI thread. The reason is that the default behaviour of the ‘await‘ keyword will let the code after it to run in the original synchronization context. You can think of the synchronization context as a thread. If you click the button, the deadlock happens because the main UI thread is waiting for the task to complete and the awaiter (line 25) is waiting for the main UI thread to be available for running the remaining code. Although there is no ‘visible’ code after ‘await‘, the awaiter still needs to let the function finish.
Resolve in Production Code
You may have not noticed this deadlock in the past because it is quite common to use the ‘async void’ event handler instead of a normal event handler when using TAP in WinForm applications. The code usually look like the following. Note the usage of async/await in both ‘button1_Click’ and ‘InvokeTask’ method.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
public partial class Form1 : Form { public Form1() { InitializeComponent(); } private async void button1_Click(object sender, EventArgs e) { await InvokeTask(); } public async Task InvokeTask() { textBox1.Text = $"Start task at {DateTime.Now.ToString("T")} and wait"; await DoLongTimeJob(); textBox1.Text = $"Task finished at {DateTime.Now.ToString("T")}"; } public static async Task DoLongTimeJob() { await Task.Delay(TimeSpan.FromSeconds(2)); } } |
The magic here is the ‘async void’ event handler. It is called differently by the runtime because it returns (not completed yet) immediately when it reaches the first ‘await’ in its function body [SO answer]. So, in production code, you should try to use async/await all the way ‘up’ to the event handlers or controllers’ actions if in a ASP.NET application.
Problem In Unit Tests
What about unit testing the DoLongTimeJob method? In NUnit, the following methods code could be used to this method.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
[Test] public void TestWithWait() { // Act var task = Form1.DoLongTimeJob(); task.Wait(); // Assert Assert.That(task.IsCompleted, Is.True); } [Test] public async Task TestWithAwait() { // Act await Form1.DoLongTimeJob(); // Can assert on the return value if the task has results. } |
This two tests runs absolutely fine if they run solely but, both of them can’t finish when they run with the following test together. (Note the following test runs before above ones).
|
1 2 3 4 5 6 7 8 9 10 11 |
[Test] public void TestRunFirst() { var newTitle = "form title"; using (var form = new Form1()) { form.Text = newTitle; Assert.That(form.Text, Is.EqualTo(newTitle)); } } |
Why does this happen? If we put a break point at the beginning of the TestWithWait method (line 3 of Code Sample 3), run the test solely and run the test with TestRunFirst. Have a look at the SynchronizationContext.Current and here are the difference. When it runs solely, the SynchronizationContext.Current is null.
However, when it runs with TestRunFirst, the value of SynchronizationContext.Current is an instance of the WindowsFormsSynchronizationContext.
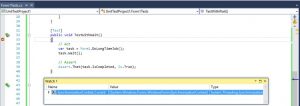
As you could remember, the test is running in the same way as in the normal event handler (not the ‘async void’ event handler).
Why does the SynchronizationContext.Current change? In WinForm applications, whenever a UI control is created, the current synchronization context will be changed to an instance of the WindowsFormssynchronizationContext. This can be simply validated by putting a break point in the Program.cs just before the form is created. You can see the synchronization context changed from null to WindowsFormssynchronizationContext.
Resove in Unit Tests
There are several ways to avoid the deadlock as long as you know the reason. The first method is to run the task on a different thread other than the current thread. (Please note that I have changed to use thread instead of synchronization context for the sake of simplicity.) This can be done by calling Task.Run method which will run the task on a thread from the thread pool.
|
1 2 3 4 5 6 7 8 9 |
[Test] public void When_DoLongTimeJob_Called_Then_Task_Can_Be_Completed() { // Act var task = Task.Run(async () => await Form1.DoLongTimeJob()); // Assert Assert.That(task.IsCompleted, Is.True); } |
The second method is to change the behaviour of the DoLongTimeJob method. Let it run the subsequent code on a different thread instead of entering to the original thread. The Task.ConfigureAwait(bool) method allows you to do this. The method will be looked like the following.
|
1 2 3 4 |
public static async Task DoLongTimeJob() { await Task.Delay(TimeSpan.FromSeconds(2)).ConfigureAwait(false); } |
Passing a false to the ConfigureAwait method. It tells the awaiter to not capture the original context and continue the execution on a different thread. It is recommended to be a good practice to always call ConfigureAwait(false) on every ‘await’ EXCEPT the remaining code after ‘await’ must be run on the original thread. For example in the InvokeTask method as shown in Code Sample 1, line 20 needs to access the UI control, so it must be run on the original thread which is the main UI thread. Note that every async methods are independent. Configuring the awaiter only affects the current ‘async’ method.
NOTE! If you want to use this method to solve the second test in Code Sample 3, you must append ConfigureAwait(false) at the end of await Form1.DoLongTimeJob() , otherwise the test still gets blocked because the execution tries to go back to the original thread which is created in WindowsFormsSynchronizationContext as well.
The last method is to explicitly clear the SynchronizationContext when running your tests. This can be done in the SetUp method before every tests are run. The current synchronization context is cleared so that it does affect the current test.
|
1 2 3 4 5 |
[SetUp] public void Setup() { SynchronizationContext.SetSynchronizationContext(null); } |
Conclusion
Any of the above methods can help you avoiding the deadlock in unit tests. Personally, I prefer to apply ConfigureAwait as much as possible because, when you create an async method, you are delegating work on a different thread and have less interests on the state of the current thread. In the unit tests, either the first method or the third method works. The third method is preferable as it does not slow the tests because of the resource allocations for additional tasks.
Oct17